一、引言
天元——棋盘正中央的星位,象征着众星烘托的北极星。在《史记历书》中:改正朔,易服色,推本天元,顺承厥意,天元有万物的本源和开始的意味。确实,在棋盘上,不存在另外任何一点与它对称,其特殊性可想而知。
在物理学,天文学,数学中,有一个“混沌“的概念,用最本质的方式来说明,就是看似极度混乱但其实有着内在规律性的现象,如一支上翘的香烟中的烟纹袅袅涡旋,又如著名的蝴蝶效应:南美洲一只蝴蝶扇一扇翅膀,就会在福罗里达引起一场暴风。这些运动在动力学上是确定的,或者说刚一开始是可控的,但在一个无论多小的扰动下,这个系统就会彻底地偏离原来的演化方向,使结果完全不可预测。
宇宙本身,就应该是最大的一个混沌系统。不仅宇宙本身,宇宙间各种各样的宏观微观系统,万事万物,莫不混沌。围棋规则简单,却变化无穷,不可预测,一着不慎,一念之间,就可以让结果翻转,也是一个混沌系统。
根据宇宙大爆炸理论,这个最大的混沌系统,可以追溯到一个具有无限大物质密度,无限大压力,无限弯曲的点——“奇点”。混沌的宇宙之浩瀚,无法用语言描述,而这个小小的奇点,在约141亿年前,用大爆炸的形式开天辟地。
同样,混沌的围棋,是否也有这样一个奇点赋予它神奇的魅力。我们想,这个点也许就是天元。所以,本文希望通过小棋盘进行分析,来说明天元的特殊地位。
为了行文的方便,我们在此做三个说明:
1)中国规则与日韩规则,一是数子,一是数目,我们无意在此讨论二者的优劣,仅仅为了证明的方便,暂采用数目法,不考虑单官影响,要求黑白双方手数一致。
2)棋谱中所有黑白棋应手均为最强手。
3)围棋的博大精深,不可能用几篇文章就洞见底蕴,因此,本文仅从小棋盘入手,来究其一二。作者作为业余围棋爱好者,举出的所有例子也不免挂一漏万,且错误之处,还望批评指正(也正是因为如此,我们在整个文章中都使用“说明”这个词而不是“证明”)。
二、天元是贴目的根源
1、偶数棋盘
很显然,对于偶数棋盘,就没有中心天元这一点,而有趣味的是,没有了天元这一点,好像贴目居然变得不必要了。
如下两图,在4路棋盘下,双方走成的一个合理的棋形,最终成“和”棋。
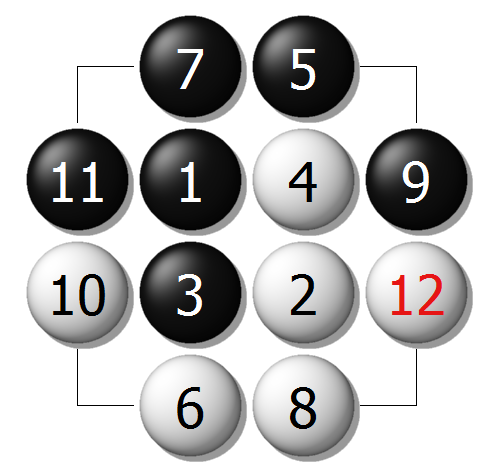
图1A、4路棋盘
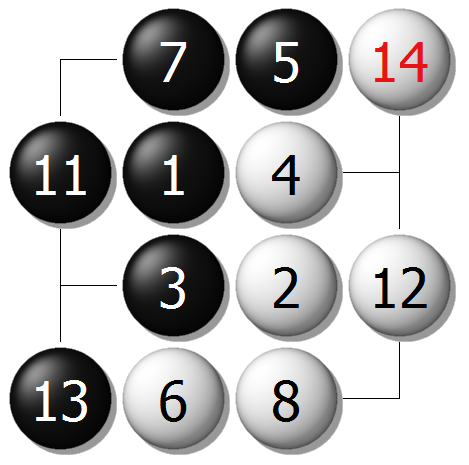
图1B、4路棋盘
再看图2的棋局,按引言中的说明,双方各为2目,也成“和”棋。
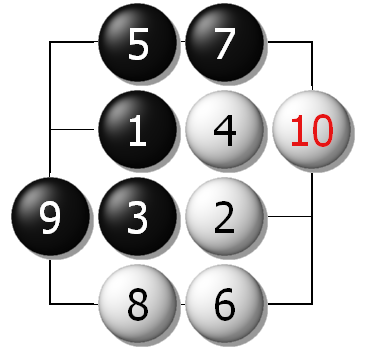
图2、4路棋盘的另一例子
2、奇数棋盘
对于三路棋盘,很容易验证:如果黑棋第一手走在天元上,得到的下面的二个典型结果图3A和图3B,均是黑比白多9目。
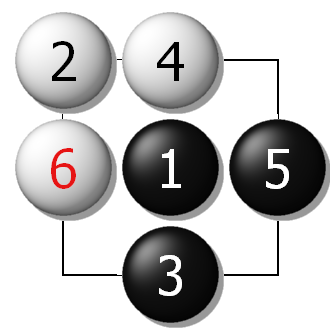
图3A、三路棋盘
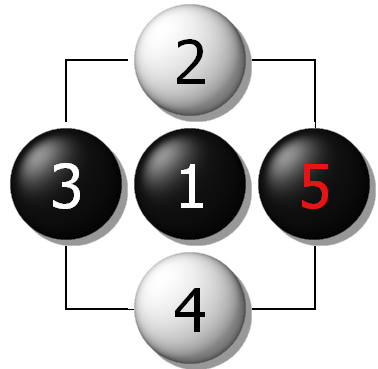
图3B、三路棋盘
为了得到猜测,我们继续研究7路棋盘,黑棋第一手仍然走在天元上,如图结果均显示出,黑比白多9目。
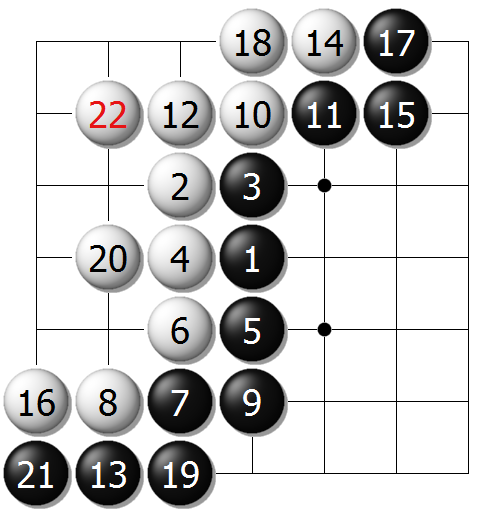
图4A、7路棋盘
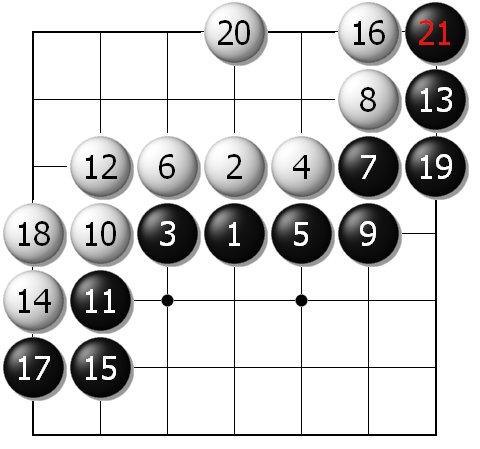
图4B 7路棋盘
由此,我们可以得出结论:围棋黑棋先行一定需要贴目(对于奇数棋盘),而且贴目的原因应该正是因为天元这一点的存在(下一节中,我们会从某种意义上再次说明这一点)。
正如本文开头所说,围棋如此复杂,小棋盘下的结论当然也不可能完全对应于大棋盘(如19路棋盘),好在本文主要的目的仅仅是想要说明天元这个点的特点。
三、反证法
由上述分析,天元这一点确实独一无二。
有了天元点(奇数棋盘)时需要贴目,没有天元点(偶数棋盘)时则无需贴目。
为了从另一个角度证明贴目正是由于天元点的原因,本节我们将用反证法再次进行说明。我们先来看看“去除天元点”后的5路棋盘的例子,如下图5二个图是两个可能的结果,双方“和”棋,即白棋只要走到对称点上,就会自然形成“和”棋。

图5A、去除“中心天元点”后的5路棋盘
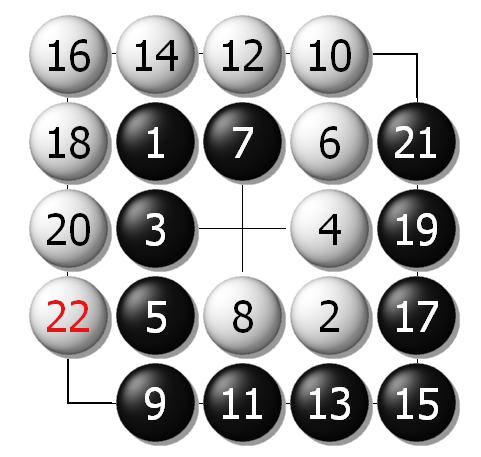
图5B、去除“中心天元点”后的5路棋盘
综上所述,天元点正是围棋中的“奇点”,有了天元时需要贴目,没有时无需贴目,即天元应是围棋贴目的原因。
四、贴9目猜想
在上述证明方法得出的对局结果中,我们惊讶地发现局终时黑棋都较白棋多9目。所以,我们想大胆地提出一个贴9目猜想,即对于“奇数棋盘”,黑棋的贴目也许应为9目。当然要想证明这个猜想,会与围棋本身一样复杂和艰难。
但我们还是想在此做一点小小的尝试:
首先,对于奇数棋盘,从3开始依次增大,贴目的比例当然是起来越小的,会迅速趋近于0,比如3路棋盘时,贴目为9目(比例则为9/9=1),5路棋盘时,贴目为25目(因白不可能活,故贴目应为25。比例则为25/25=1),7路棋盘时,当贴目为9目时,其比例为9/49=0.2。
那么随着棋盘尺寸的扩大,贴目值的变化趋势就会有三种可能性:变大、变小和不变。根据我们的对局经验,加上考虑到执黑先行贴目的艰难,变大的可能性最小。
下面我们通过二个例子来说明,从七路棋盘到九路棋盘,贴目会不会变小?
由于七路以上棋盘,很难穷尽黑白最佳对局,所以笔者想出一个类似“座子”式简化棋盘的方法,即将棋盘简化为双方均衡的形式,来减少棋局的变化。
例1、网状座子简化后的七路棋盘。
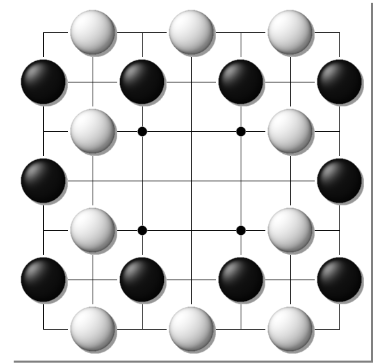
图6A、网络状的开局
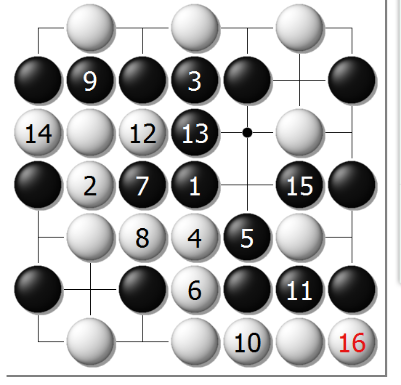
图6B、双方最强应对后的结果
例2、简化后的七路棋盘。
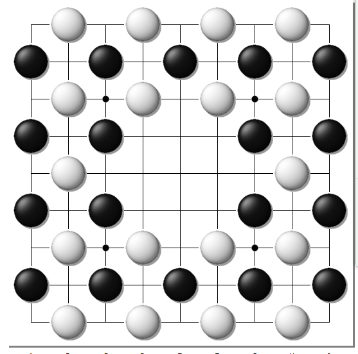
图7A、网络状的开局
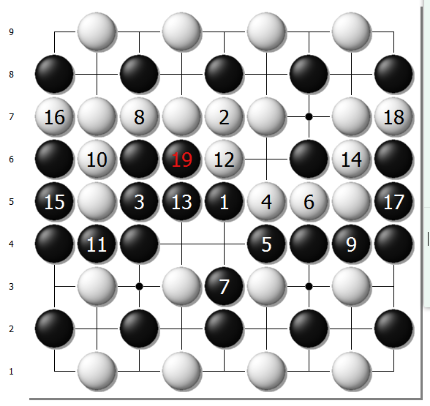
图7B、双方最强应对后的结果
利用简化后的棋盘,我们第一手走到天元点,然后找出大约是黑白双方最佳下发的棋局如下,其中黑棋依然领先白棋9目:
以上二个例子都说明对于9路棋盘而言,贴目并不随着棋盘的增大而变小。
另一方面,数学和自然界中的奇点概念是与尺寸无关的,从这个意义上来讲,因为贴目是因奇点而起,当然也就不应该与棋盘的尺寸有关。
总之,围棋中先行方黑棋的贴目也许正好就是9目,暗合九九和一之道。
后记
2014年11月30日,一代宗师吴清源先生离世,从此人间少了一位围棋大师,而宇宙天堂间同时也多了一位真理的探索者。
吴先生一生追求围棋的真理,敢于创新,对于第一手走天元也有过尝试。
谨以此文纪念吴先生。
备注:本文已刊发于《围棋天地》2015年第9期






